（9）式で与えられた入射波に対して、境界値問題（3）〜（7）式を解くことによってdiffraction potentialφdが求められる。

［radiation問題］

浮体を弾性体として、運動および変形によって発生する放射波（radiation wave）を求める問題を考える。

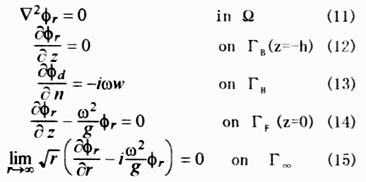
ここに w（x,y）は、浮体のz方向変位（たわみ）であり、浮体下面のn方向変位に対応している。diffraction問題とradiation問題は、物体表面条件のみが異なる形となっているので、物体表面条件以外の式を自動的に満たすようなGreen関数（基本解）を用いて境界要素法によって定式化する事にすれば、いずれの問題も流体部に関しては共通の係数マトリックスを用いることができる。本研究では、浮体の底面に双一次の境界要素を設置して離散化を行っている。本研究には、Garrison［8］によって与えられたGreen関数を用いている［9］。

2.3. 圧力変動と速度ポテンシャルとの関係

拡張されたBernoulliの定理（圧カ方程式）から圧力Pと速度ポテンシャルΦの関係式が導かれる。非線形項を無視すると圧力は次式で表される。

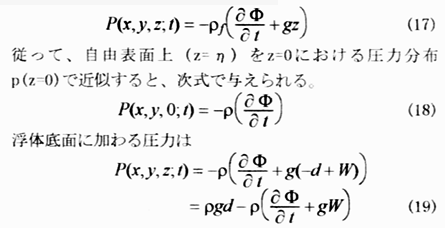
ここにdは静水中の浮体の喫水。

しかし、右辺第1項は静水中の静水圧であり、その他の部分の第1項は動的流体力、第2項は静的変動圧力である。速度ポテンシャルΦが調和変動ずる量であるとき、

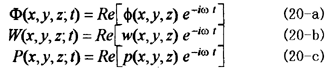
と表すことができるので、時間項を分離して表現すれば、次式となる。

浮体表面上に加わる変動圧力

p（x ,y, z）＝iωρφ（x, y, z）−gw（x, y, z） （21）

自由表面上の変動圧力

p（x,y0）＝iωρφ（x, y, 0） （22）

ところで（1）式右辺の等価外力ベクトルは、上記の離散化を行うことによって次式の形で表される。

f＝iρfω・Cp（φi+φd+φr）-ρfg・Cwv （22）

流体部の境界要素と（1）式の構造部のマトリックス方程式により最終的に、構造部に対して次式が得られる。

[（K+Kw）-ω2M]v−iρfωCpφr＝ipfωCp（φi+φd） （23）

ここに、Kwは、（17）式右辺第2項から導かれる、浮力バネによる等価付加剛性マトリックスである。一方、構造部の有限要素と、流体部の境界要素との間にインターフェースを考慮して、radiation問題は、

Hφr＝−iωGAv （24）

となる。（23）、（24）式をまとめて表すと、

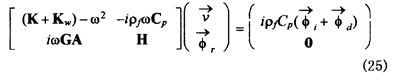
この複素連立1次方程式を解くことにより、解が得られる。本研究では、境界要素内の積分に関しては4×4＝16点のGauss積分点を設置し、特異点となる節点を含む要素に関する積分にはサブ要素分割法［10］を用いて数値積分の精度を確保している。

3. 数値計算結果および考察

3.1. Green関数について

波長を固定して水深を変化させたときのグリーン関数G振幅の相違を調べた。水深が小さくなると水底の影響で、グリーン関数の振幅が大きくなる傾向になっている。水深が波長の半分以上になると余り相違が無くなる。また、水深波長の比hλの大きさが0.5または0.6以上では、無限水深とほぼ等しいＧの値になっているので、これ以上の水深に対しては無限水深の場合のGreen関数を用いても良いと考えられる。物理的に表現すれば、水深が半波長以上であれば、ほぼ無限水深と見なせるという事ができるであろう。

3.2diffraction問題の計算結果と収束性

（5）式とマトリックス境界要素方程式から次式を解くことによってφdを求められる。

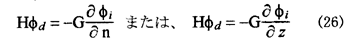
計算にはTable1に示す長き2500m幅500mの浮体を想定して計算を行っている。φdの分布形状の最も変化の大きい入射側のコーナー一部の節点におけるφdの値の収束性を

前ページ　　　目次へ　　　次ページ